
图1
从以上叙述可以看出,对于一个确定的样本,进行多次试验,再根据这些试验的某个统计量(比如平均值)的多次结果求平均,用于对总体的分布参数(期望u)进行估计,如果两者相等的话,那么就是无偏估计,否则就是有偏估计。

图2
这个例子的意思是,由于X1既可以代表一个随机变量,又可以代表这个随机变量某次试验的取值,所以,通过对这个随机变量的多次试验,它的期望会等于总体的期望,因此是无偏估计。
那么,有了上述的理解以后,显然X2,X3,。。。。。。。等等,它们多次试验结果的期望都应该等于总体期望u,那下图的结果就是显而易见的:

再看有偏估计:
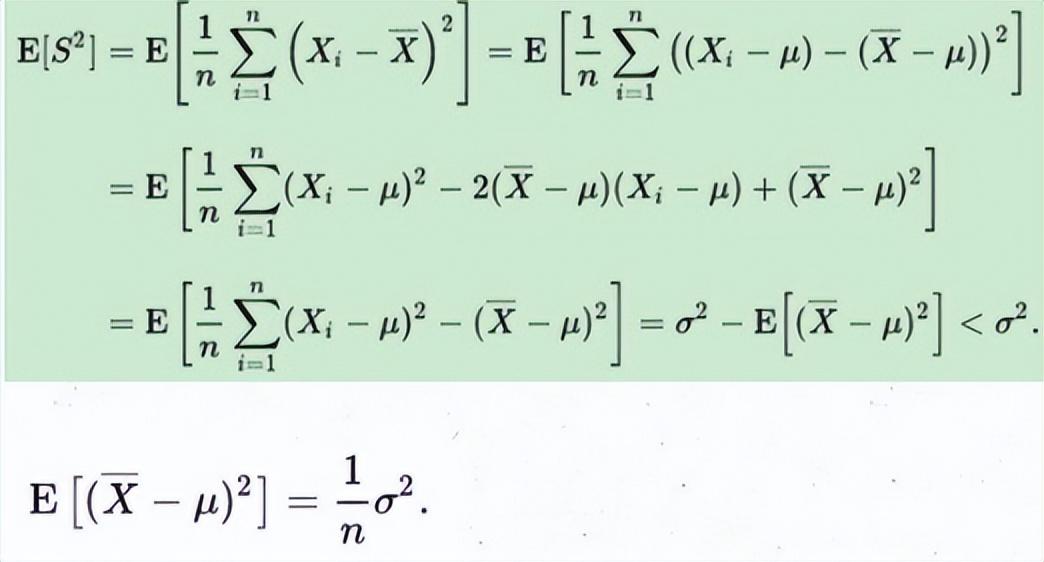
图3

图4
从图3和图4可以看出,当用样本方差

来估计总体方差
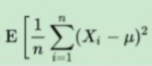
的时候,当样本确定的前提下,即使试验次数n为无穷大,两者之间还是存在着误差
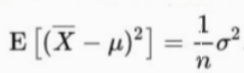
从图4可以看出,其原因就是样本均值不等于总体均值。
因此,可以总结如下:
当用样本统计量去估计某个总体统计量的时候,在样本确定的前提下,如果试验次数无穷大的时候两者相等,就是无偏估计,不等的时候就是有偏估计。