什么是有理数的定义（初中数学有理数完全归纳）

有理数

【思维导图】

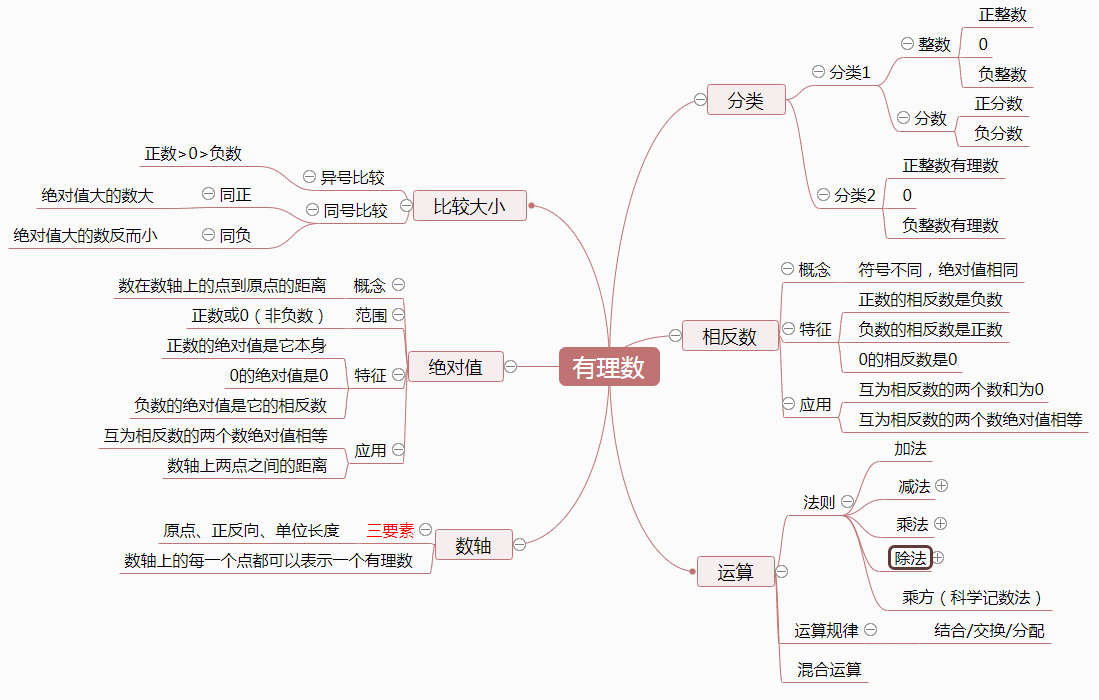
【知识要点】

知识点一 有理数基础概念

• 有理数（概念理解）

正数：大于0的数叫做正数。

负数：正数前面加上符号“-”的数叫负数。

有理数的分类（两种）（见思维导图）

• 数轴

规定了原点、正方向、单位长度的直线叫做数轴。

• 数轴的三要素：原点、正方向、单位长度（重点）

任何有理数都可以用数轴上的点表示。

• 数轴上的点表示的数从左到右依次增大；原点左边的数是负数，原点右边的数是正数.

【注意】

1. 数轴是一条直线，可向两段无限延伸。
2. 在数轴上原点，正方向，单位长度的选取需根据实际情况而定。

• 相反数

只有符号不同的两个数叫做互为相反数.（绝对值相等，符号不同的两个数叫做互为相反数）

• 绝对值

绝对值的概念：一班数轴上表示a的数与原点之间的距离叫做数a的绝对值。

绝对值的意义：

正数的绝对值是它本身；

负数的绝对值是它的相反数；

0的绝对值是0。

（互为相反数的两个数的绝对值相等。）

• 比较大小

1）数轴上两个点表示的数，右边的总比左边的大。

2）正数大于0，负数小于0，正数大于负数。

3）两个负数比较，绝对值大的反而小。

4）两个正数比较，绝对值大的反而大。

常用方法：数轴比较法、差值比较法、商值比较法、绝对值比较法等。

知识点二 有理数四则运算

• 有理数的加法（重点）

有理数的加法法则：（先确定符号，再算绝对值）

1.同号两数相加，取相同的符号，并把绝对值相加；

2.异号两数相加，绝对值不相等时，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值；

3.互为相反数的两个数相加得0；（如果两个数的和为0，那么这两个数互为相反数）

4.一个数同0相加，仍得这个数。

有理数的加法运算律：

加法交换律：两个数相加，交换加数的位置，和不变。

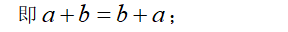
加法结合律：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。

• 有理数的减法

有理数的减法法则：

减去一个数等于加上这个数的相反数。即

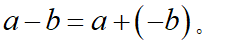
注：两个变化：减号变成加号；减数变成它的相反数。

• 有理数的加减混合运算

规则：运用减法法则将加减混合运算统一为加法进行运算

步骤：（1）减法化加法；

（2）省略括号和加号；

（3）运用加法运算律使计算简便；

（4）运用有理数加法法则进行计算。

注：运用加法运算律时，可按如下几点进行：

（1）同号的先结合；

（2）同分母的分数或者比较容易通分的分数相结合；

（3）互为相反数的两数相结合；

（4）能凑成整数的两数相结合；

（5）带分数一般化为假分数或者分为整数和分数两部分，再分别相加。

• 有理数的乘法（重点）

有理数的乘法法则：

（1）两数相乘，同号得正，异号得负，并把绝对值相乘。

（2）任何数同0相乘，都得0.

多个有理数相乘的法则及规律：

1. 几个不是0的数相乘，负因数的个数是奇数时，积是负数；

负因数的个数是偶数时，积是正数。

确定符号后，把各个因数的绝对值相乘。

（2）几个数相乘，有一个因数为0，积为0；反之，如果积为0，那么至少有一个因数是0.

注：带分数与分数相乘时，通常把带分数化成假分数，再与分数相乘。

• 有理数的乘法运算律

乘法交换律：两个数相乘，交换因数的位置，积相等。

乘法结合律：三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积相等。

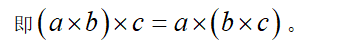
乘法分配律：一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加。

• 有理数的除法

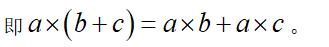
有理数除法法则：

1. 除以一个不为0的数，等于乘以这个数的倒数。

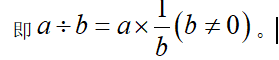
（2）两数相除（被除数不为0），同号得正，异号得负，并把绝对值相除。

0除以任何不为0的数，都得0。

步骤：先确定商的符号，再算出商的绝对值。

• 有理数的乘除混合运算

运算顺序：从左往右进行，将除法化成乘法后，进行约分计算。

（注：带分数应首先化为假分数进行运算）

• 有理数的四则混合运算

运算顺序：先乘除，后加减，有括号要先算括号里面的。

注：除法一般先化为乘法，带分数化为假分数，合理使用运算律

知识点三 有理数的乘方

• 乘方（重点）

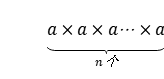
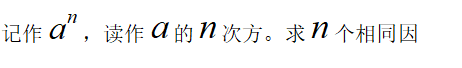
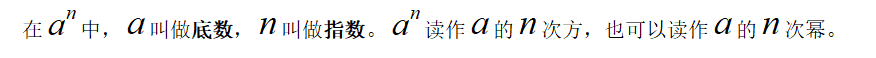
当底数为分数时，要先用括号将底数括上，再在其右上角写指数，指数要写的小些。

乘方的规律：

负数的奇次幂是负数，负数的偶次幂是正数。

正数的任何次幂都是正数，0的任何正整数次幂都是0.

有理数乘方的运算方法：

1. 根据乘方的符号规律确定结果的符号。
2. 计算结果的绝对值。

• 有理数的混合运算

运算顺序：（1）先乘方，再乘除，最后加减；

（2）同级运算,从左到右进行；

（3）如有括号，先算括号里的，按小括号、中括号、大括号的顺序。

• 科学记数法

• 近似数和有效数字

在实际问题中，由“四舍五入”得到的数或大约估计的数都是近似数。（近似数小数点后的末位数是0的，不能去掉0.）

一个近似数从左边第一位非0的数字起，到末位数字止，所有的数字都是这个数的有效数字。一个近似数有几个有效数字，就称这个近似数保留几个有效数字。

精确度：表示一个近似数与准确数的接近程度。一个近似数，四舍五入到哪一位，就称这个数精确到哪一位。

【考查题型】

考查题型一 有理数概念理解

【解题思路】理解有理数的定义，熟练掌握与正确理解有理数的分类是解题的关键。

考查题型二 用数轴上的点表示有理数

【解题思路】在数轴上，原点左边的点表示的是负数，原点右边的点表示的是正数，右边的点表示的数比左边的点表示的数大.

考查题型三 求一个数的相反数

【解题思路】理解相反数的概念

考查题型四 求一个数的绝对值

【解题思路】一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．

考查题型五 有理数比较大小

【解题思路】理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小。

考查题型六 有理数的加减乘除混合运算

【解题思路】针对有理数的混合运算，掌握有理数的运算顺序和各个运算法则是解题关键．

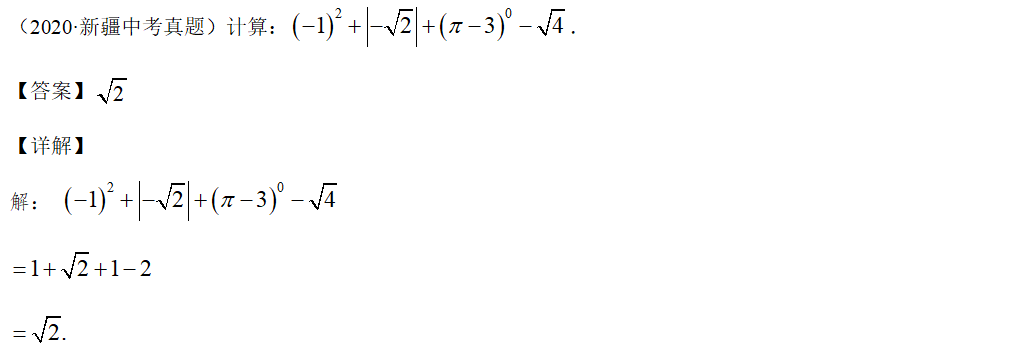
考查题型七 科学记数法